Сравнивать величины и количества при решении практических задач приходилось ещё с древних времён. Тогда же появились и такие слова, как больше и меньше, выше и ниже, легче и тяжелее, тише и громче, дешевле и дороже и т.д., обозначающие результаты сравнения однородных величин.

Понятия больше и меньше возникли в связи со счётом предметов, измерением и сравнением величин. Например, математики Древней Греции знали, что сторона любого треугольника меньше суммы двух других сторон и что против большего угла в треугольнике лежит большая сторона. Архимед, занимаясь вычислением длины окружности, установил, что периметр всякого круга равен утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых диаметра.

Символически записывать соотношения между числами и величинами с помощью знаков > и b. Записи, в которых два числа соединены одним из знаков: > (больше), С числовыми неравенствами вы встречались и в младших классах. Знаете, что неравенства могут быть верными, а могут быть и неверными. Например, \(\frac{1}{2} > \frac{1}{3} \) верное числовое неравенство, 0,23 > 0,235 - неверное числовое неравенство.

Неравенства, в которые входят неизвестные, могут быть верными при одних значениях неизвестных и неверными при других. Например, неравенство 2x+1>5 верное при х = 3, а при х = -3 - неверное. Для неравенства с одним неизвестным можно поставить задачу: решить неравенство. Задачи решения неравенств на практике ставятся и решаются не реже, чем задачи решения уравнений. Например, многие экономические проблемы сводятся к исследованию и решению систем линейных неравенств. Во многих разделах математики неравенства встречаются чаще, чем уравнения.

Некоторые неравенства служат единственным вспомогательным средством, позволяющим доказать или опровергнуть существование определённого объекта, например, корня уравнения.

Числовые неравенства

Вы умеете сравнивать целые числа, десятичные дроби. Знаете правила сравнения обыкновенных дробей с одинаковыми знаменателями, но разными числителями; с одинаковыми числителями, но разными знаменателями. Здесь вы научитесь сравнивать любые два числа с помощью нахождения знака их разности.

Сравнение чисел широко применяется на практике. Например, экономист сравнивает плановые показатели с фактическими, врач сравнивает температуру больного с нормальной, токарь сравнивает размеры вытачиваемой детали с эталоном. Во всех таких случаях сравниваются некоторые числа. В результате сравнения чисел возникают числовые неравенства.

Определение. Число а больше числа b, если разность а-b положительна. Число а меньше числа b, если разность а-b отрицательна.

Если а больше b, то пишут: а > b; если а меньше b, то пишут: а Таким образом, неравенство а > b означает, что разность а - b положительна, т.е. а - b > 0. Неравенство а Для любых двух чисел а и b из следующих трёх соотношений a > b, a = b, a Сравнить числа а и b - значит выяснить, какой из знаков >, = или Теорема. Если a > b и Ь > с, то а > с.

Теорема. Если к обеим частям неравенства прибавить одно и то же число, то знак неравенства не изменится.
Следствие. Любое слагаемое можно перенести из одной части неравенства в другую, изменив знак этого слагаемого на противоположный.

Теорема. Если обе части неравенства умножить на одно и то же положительное число, то знак неравенства не изменится. Если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Следствие. Если обе части неравенства разделить на одно и то же положительное число, то знак неравенства не изменится. Если обе части неравенства разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.

Вы знаете, что числовые равенства можно почленно складывать и умножать. Далее вы научитесь выполнять аналогичные действия с неравенствами. Умения почленно складывать и умножать неравенства часто применяются на практике. Эти действия помогают решать задачи оценивания и сравнения значений выражений.

При решении различных задач часто приходится складывать или умножать почленно левые и правые части неравенств. При этом иногда говорят, что неравенства складываются или умножаются. Например, если турист прошёл в первый день более 20 км, а во второй - более 25 км, то можно утверждать, что за два дня он прошёл более 45 км. Точно так же если длина прямоугольника меньше 13 см, а ширина меньше 5 см, то можно утверждать, что площадь этого прямоугольника меньше 65 см2.

При рассмотрении этих примеров применялись следующие теоремы о сложении и умножении неравенств:

Теорема. При сложении неравенств одинакового знака получается неравенство того же знака: если а > b и c > d, то a + c > b + d.

Теорема. При умножении неравенств одинакового знака, у которых левые и правые части положительны, получается неравенство того же знака: если а > b, c > d и а, b, с, d - положительные числа, то ac > bd.

Неравенства со знаком > (больше) и 1/2, 3/4 b, c Наряду со знаками строгих неравенств > и Точно так же неравенство \(a \geq b \) означает, что число а больше или равно b, т. е. а не меньше b.

Неравенства, содержащие знак \(\geq \) или знак \(\leq \), называют нестрогими. Например, \(18 \geq 12 , \; 11 \leq 12 \) - нестрогие неравенства.

Все свойства строгих неравенств справедливы и для нестрогих неравенств. При этом если для строгих неравенств противоположными считались знаки > и Вы знаете, что для решения ряда прикладных задач приходится составлять математическую модель в виде уравнения или системы уравнений. Далее вы узнаете, что математическими моделями для решения многих задач являются неравенства с неизвестными. Будет введено понятие решения неравенства и показано, как проверить, является ли данное число решением конкретного неравенства.

Неравенства вида
\(ax > b, \quad ax в которых а и b - заданные числа, а x - неизвестное, называют линейными неравенствами с одним неизвестным .

Определение. Решением неравенства с одним неизвестным называется то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство. Решить неравенство - это значит найти все его решения или установить, что их нет.

Решение уравнений вы осуществляли путём приведения их к простейшим уравнениям. Аналогично при решении неравенств их стремятся с помощью свойств привести к виду простейших неравенств.

Решение неравенств второй степени с одной переменной

Неравенства вида
\(ax^2+bx+c >0 \) и \(ax^2+bx+c где x - переменная, a, b и c - некоторые числа и \(a \neq 0 \), называют неравенствами второй степени с одной переменной .

Решение неравенства
\(ax^2+bx+c >0 \) или \(ax^2+bx+c можно рассматривать как нахождение промежутков, в которых функция \(y= ax^2+bx+c \) принимает положительные или отрицательные значения. Для этого достаточно проанализировать, как расположен график функции \(y= ax^2+bx+c \) в координатной плоскости: куда направлены ветви параболы - вверх или вниз, пересекает ли парабола ось x и если пересекает, то в каких точках.

Алгоритм решения неравенств второй степени с одной переменной:
1) находят дискриминант квадратного трехчлена \(ax^2+bx+c \) и выясняют, имеет ли трехчлен корни;
2) если трехчлен имеет корни, то отмечают их на оси x и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при a > 0 или вниз при a 0 или в нижней при a 3) находят на оси x промежутки, для которых точки параболы расположены выше оси x (если решают неравенство \(ax^2+bx+c >0 \)) или ниже оси x (если решают неравенство
\(ax^2+bx+c Решение неравенств методом интервалов

Рассмотрим функцию
f(x) = (х + 2)(х - 3)(х - 5)

Областью определения этой функции является множество всех чисел. Нулями функции служат числа -2, 3, 5. Они разбивают область определения функции на промежутки \((-\infty; -2), \; (-2; 3), \; (3; 5) \) и \((5; +\infty) \)

Выясним, каковы знаки этой функции в каждом из указанных промежутков.

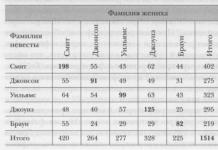
Выражение (х + 2)(х - 3)(х - 5) представляет собой произведение трех множителей. Знак каждого из этих множителей в рассматриваемых промежутках указан в таблице:

Вообще пусть функция задана формулой
f(x) = (x-x 1)(x-x 2) ... (x-x n),
где x–переменная, а x 1 , x 2 , ..., x n – не равные друг другу числа. Числа x 1 , x 2 , ..., x n являются нулями функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль ее знак изменяется.

Это свойство используется для решения неравенств вида
(x-x 1)(x-x 2) ... (x-x n) > 0,
(x-x 1)(x-x 2) ... (x-x n) где x 1 , x 2 , ..., x n - не равные друг другу числа

Рассмотренный способ решения неравенств называют методом интервалов.

Приведем примеры решения неравенств методом интервалов.

Решить неравенство:

\(x(0,5-x)(x+4) Очевидно, что нулями функции f(x) = x(0,5-x)(x+4) являются точки \(x=0, \; x=\frac{1}{2} , \; x=-4 \)

Наносим на числовую ось нули функции и вычисляем знак на каждом промежутке:

Выбираем те промежутки, на которых функция меньше или равна нулю и записываем ответ.

Ответ:
\(x \in \left(-\infty; \; 1 \right) \cup \left[ 4; \; +\infty \right) \)

Поле действительных чисел обладает свойством упорядоченности (п. 6, стр. 35): для любых чисел а, b имеет место одно и только одно из трех соотношений: или . При этом запись а > b означает, что разность положительна, а запись разность отрицательна. В отличие от поля действительных чисел, поле комплексных чисел не упорядочивается: для комплексных чисел понятия «больше» и «меньше» не определяются; поэтому в данной главе рассматриваются только действительные числа.

Соотношения назовем неравенствами, числа а и b - членами (или частями) неравенства, знаки > (больше) и Неравенства а > b и с > d называются неравенствами одинакового (или одного и того же) смысла; неравенства а > b и с Из определения неравенства сразу следует, что

1) любое положительное число больше нуля;

2) любое отрицательное число меньше нуля;

3) любое положительное число больше любого отрицательного числа;

4) из двух отрицательных чисел больше то, абсолютная величина которого меньше.

Все эти утверждения допускают простое геометрическое истолкование. Пусть положительное направление числовой оси идет вправо от начальной точки; тогда, каковы бы ни были знаки чисел, большее из них изображается точкой, лежащей правее точки, изображающей меньшее число.

Неравенства обладают следующими основными свойствами.

1. Несимметричность (необратимость): если , то , и обратно.

Действительно, если разность положительна, то разность отрицательна. Говорят, что при перестановке членов неравенства надо смысл неравенства изменить на противоположный.

2. Транзитивность: если , то . Действительно, из положительности разностей следует и положительность

Кроме знаков неравенства применяют также знаки неравенства и Они определяются следующим образом: запись означает, что либо либо Поэтому, например, можно писать , а также . Обычно неравенства, записанные с помощью знаков называют строгими неравенствами, а записанные с помощью знаков нестрогими неравенствами. Соответственно и сами знаки называют знаками строгого или нестрогого неравенства. Свойства 1 и 2, рассмотренные выше, верны и для нестрогих неравенств.

Рассмотрим теперь действия, которые можно производить над одним или несколькими неравенствами.

3. От прибавления к членам неравенства одного и того же числа смысл неравенства не изменяется.

Доказательство. Пусть даны неравенство и произвольное число . По определению разность положительна. Прибавим к этому числу два противоположных числа от чего оно не изменится, т. е.

Это равенство можно переписать так:

Из этого следует, что разность положительна, т. е. что

а это и надо было доказать.

На этом основана возможность перекоса любого члена неравенства из одной его части в другую с противоположным знаком. Например, из неравенства

следует, что

4. При умножении членов неравенства на одно и то же положительное число смысл неравенства не изменяется; при умножении членов неравенства на одно и то же отрицательное число смысл неравенства изменяется на противоположный.

Доказательство. Пусть тогда Если то так как произведение положительных чисел положительно. Раскрыв скобки в левой части последнего неравенства, получим , т. е. . Аналогичным образом рассматривается случай .

Точно такой же вывод можно сделать и относительно деления частей неравенства на какое-либо отличное от нуля число, так как деление на число равносильно умножению на число а числа имеют одинаковые знаки.

5. Пусть члены неравенства положительны. Тогда при возведении его членов в одну и ту же положительную степень смысл неравенства не изменяется.

Доказательство. Пусть этом случае по свойству транзитивности и . Тогда в силу монотонного возрастания степенной функции при и положительном будем иметь

В частности, если где -натуральное число, то получим

т. е. при извлечении корня из обеих частей неравенства с положительными членами смысл неравенства не изменяется.

Пусть члены неравенства отрицательны. Тогда нетрудно доказать, что при возведении его членов в нечетную натуральную степень смысл неравенства не изменится, а при возведении в четную натуральную степень изменится на противоположный. Из неравенств с отрицательными членами можно также извлекать корень нечетной степени.

Пусть, далее, члены неравенства имеют разные знаки. Тогда при возведении его в нечетную степень смысл неравенства не изменится, а при возведении в четную степень о смысле получающегося неравенства ничего определенного в общем случае сказать нельзя. В самом деле, при возведении числа в нечетную степень знак числа сохраняется и поэтому смысл неравенства не изменяется. При возведении же неравенства в четную степень образуется неравенство с положительными членами, и его смысл будет зависеть от абсолютных величин членов исходного неравенства может получиться неравенство того же смысла, что и исходное, неравенство противоположного смысла и даже равенство!

Все сказанное о возведении неравенств в степень полезно проверить на следующем примере.

Пример 1. Возвести в указанную степень следующие неравенства, изменив в случае необходимости знак неравенства на противоположный или на знак равенства.

а) 3 > 2 в степень 4; б) в степень 3;

в) в степень 3; г) в степень 2;

д) в степень 5; е) в степень 4;

ж) 2 > -3 в степень 2; з) в степень 2,

6. От неравенства можно перейти к неравенству между если члены неравенства оба положительны или оба отрицательны, то между их обратными величинами имеется неравенство противоположного смысла:

Доказательство. Если а и b - одного знака, то их произведение положительно. Разделим на неравенство

т. е. , что и требовалось получить.

Если члены неравенства имеют противоположные знаки, то неравенство между их обратными величинами имеет тот же смысл, так как знаки обратных величин те же, что и знаки самих величин.

Пример 2. Проверить последнее свойство 6 на следующих неравенствах:

7. Логарифмирование неравенств можно производить лишь в случае, когда члены неравенств положительны (отрицательные числа и нуль логарифмов не имеют).

Пусть . Тогда при будет

а при будет

Правильность этих утверждений основана на монотонности логарифмической функции, которая возрастает, если основание и убывает при

Итак, при логарифмировании неравенства, состоящего из положительных членов, по основанию, большему единицы, образуется неравенство того же смысла, что и данное, а при логарифмировании его по положительному основанию, меньшему единицы, - неравенство противоположного смысла.

8. Если , то если , но , то .

Это сразу следует из свойств монотонности показательной функции (п. 42), которая возрастает в случае и убывает, если

При почленном сложении неравенств одного и того же смысла образуется неравенство того же смысла, что и данные.

Доказательство. Докажем это утверждение для двух неравенств, хотя оно верно для любого количества складываемых неравенств. Пусть даны неравенства

По определению числа будут положительными; тогда положительной оказывается и их сумма, т. е.

Группируя иначе слагаемые, получим

и, следовательно,

а это и надо было доказать.

Нельзя сказать Ничего определенного в общем случае о смысле неравенства, получающегося при сложении двух или нескольких неравенств разного смысла.

10. Если из одного неравенства почленно вычесть другое неравенство противоположного смысла, то образуется неравенство того же смысла, что и первое.

Доказательство. Пусть даны два неравенства разного смысла. Второе из них по свойству необратимости можно переписать так: d > с. Сложим теперь два неравенства одинакового смысла и получим неравенство

того же смысла. Из последнего находим

а это и надо было доказать.

Нельзя сказать ничего определенного в общем случае о смысле неравенства, получающегося при вычитании из одного неравенства другого неравенства того же смысла.

С неравенствами мы познакомились в школе, где применяем числовые неравенства. В данной статье рассмотрим свойства числовых неравенств, не которых строятся принципы работы с ними.

Свойства неравенств аналогичны свойствам числовых неравенств. Будут рассмотрены свойства, его обоснования, приведем примеры.

Yandex.RTB R-A-339285-1

Числовые неравенства: определение, примеры

При введении понятия неравенства имеем, что их определение производится по виду записи. Имеются алгебраические выражения, которые имеют знаки ≠ , < , > , ≤ , ≥ . Дадим определение.

Определение 1

Числовым неравенством называют неравенство, в записи которого обе стороны имеют числа и числовые выражения.

Числовые неравенства рассматриваем еще в школе после изучения натуральных чисел. Такие операции сравнения изучаются поэтапно. Первоначальные имею вид 1 < 5 , 5 + 7 > 3 . После чего правила дополняются, а неравенства усложняются, тогда получаем неравенства вида 5 2 3 > 5 , 1 (2) , ln 0 . 73 - 17 2 < 0 .

Свойства числовых неравенств

Чтобы правильно работать с неравенствами, необходимо использовать свойства числовых неравенств. Они идут из понятия неравенства. Такое понятие задается при помощи утверждения, которое обозначается как «больше» или «меньше».

Определение 2

• число a больше b , когда разность a - b – положительное число;
• число a меньше b , когда разность a - b – отрицательное число;
• число a равно b , когда разность a - b равняется нулю.

Определение используется при решении неравенств с отношениями «меньше или равно», «больше или равно». Получаем, что

Определение 3

• a больше или равно b , когда a - b является неотрицательным числом;
• a меньше или равно b , когда a - b является неположительным числом.

Определения будут использованы при доказательствах свойств числовых неравенств.

Основные свойства

Рассмотрим 3 основные неравенства. Использование знаков < и > характерно при свойствах:

Определение 4

• антирефлексивности , которое говорит о том, что любое число a из неравенств a < a и a > a считается неверным. Известно, что для любого a имеет место быть равенство a − a = 0 , отсюда получаем, что а = а. Значит, a < a и a > a неверно. Например, 3 < 3 и - 4 14 15 > - 4 14 15 являются неверными.
• ассиметричности . Когда числа a и b являются такими, что a < b , то b > a , и если a > b , то b < a . Используя определение отношений «больше», «меньше» обоснуем его. Так как в первой части имеем, что a < b , тогда a − b является отрицательным числом. А b − a = − (a − b) положительное число, потому как число противоположно отрицательному числу a − b . Отсюда следует, что b > a . Аналогичным образом доказывается и вторая его часть.

Пример 1

Например, при заданном неравенстве 5 < 11 имеем, что 11 > 5 , значит его числовое неравенство − 0 , 27 > − 1 , 3 перепишется в виде − 1 , 3 < − 0 , 27 .

Перед тем, как перейти к следующему свойству, заметим, что при помощи ассиметричности можно читать неравенство справа налево и наоборот. Таким образом, числовое неравенство можно изменять и менять местами.

Определение 5

• транзитивности . Когда числа a , b , c соответствуют условию a < b и b < c , тогда a < c , и если a > b и b > c , тогда a > c .

Доказательство 1

Первое утверждение можно доказать. Условие a < b и b < c означает, что a − b и b − c являются отрицательными, а разность а - с представляется в виде (a − b) + (b − c) , что является отрицательным числом, потому как имеем сумму двух отрицательных a − b и b − c . Отсюда получаем, что а - с является отрицательным числом, а значит, что a < c . Что и требовалось доказать.

Аналогичным образом доказывается вторая часть со свойством транизитивности.

Пример 2

Разобранное свойство рассматриваем на примере неравенств − 1 < 5 и 5 < 8 . Отсюда имеем, что − 1 < 8 . Аналогичным образом из неравенств 1 2 > 1 8 и 1 8 > 1 32 следует, что 1 2 > 1 32 .

Числовые неравенства, которые записываются с помощью нестрогих знаков неравенства, обладают свойством рефлексивности, потому как a ≤ a и a ≥ a могут иметь случай равенства а = а. им присуща ассиметричность и транзитивность.

Определение 6

Неравенства, имеющие в записи знаки ≤ и ≥ , имеют свойства:

• рефлексивности a ≥ a и a ≤ a считаются верными неравенствами;
• антисимметричности, когда a ≤ b , тогда b ≥ a , и если a ≥ b , тогда b ≤ a .
• транзитивности, когда a ≤ b и b ≤ c , тогда a ≤ c , а также, если a ≥ b и b ≥ c , то тогда a ≥ c .

Доказательство производится аналогичным образом.

Другие важные свойства числовых неравенств

Для дополнения основных свойств неравенств используются результаты, которые имеют практическое значение. Применяется принцип метода оценка значений выражений, на которых и базируются принципы решения неравенств.

Данный пункт раскрывает свойства неравенств для одного знака строгого неарвенства. Аналогично производится для нестрогих. Рассмотрим на примере, сформулировав неравенство если a < b и c являются любыми числами, то a + c < b + c . Справедливыми окажутся свойства:

• если a > b , то a + c > b + c ;
• если a ≤ b , то a + c ≤ b + c ;
• если a ≥ b , то a + c ≥ b + c .

Для удобного представления дадим соответствующее утверждение, которое записывается и приводятся доказательства, показываются примеры использования.

Определение 7

Прибавление или вычисления числа к обеим сторонам. Иначе говоря, когда a и b соответствуют неравенству a < b , тогда для любого такого числа имеет смысл неравенство вида a + c < b + c .

Доказательство 2

Чтобы доказать это, необходимо, чтобы уравнение соответствовало условию a < b . Тогда (a + c) − (b + c) = a + c − b − c = a − b . Из условия a < b получим, что a − b < 0 . Значит, (a + c) − (b + c) < 0 , откуда a + c < b + c . Множество действительных числе могут быть изменены с помощью прибавления противоположного числа – с.

Пример 3

К примеру, если обе части неравенства 7 > 3 увеличиваем на 15 , тогда получаем, что 7 + 15 > 3 + 15 . Это равно 22 > 18 .

Определение 8

Когда обе части неравенства умножить или разделить на одно и то же число c , получим верное неравенство. Если взять число c отрицательным, то знак поменяется на противоположный. Иначе это выглядит так: для a и b неравенство выполняется, когда a < b и c являются положительными числами, то a· c < b · c , а если v является отрицательным числом, тогда a · c > b · c .

Доказательство 3

Когда имеется случай c > 0 , необходимо составить разность левой и правой частей неравенства. Тогда получаем, что a · c − b · c = (a − b) · c . Из условия a < b , то a − b < 0 , а c > 0 , тогда произведение (a − b) · c будет отрицательным. Отсюда следует, что a · c − b · c < 0 , где a · c < b · c . Другая часть доказывается аналогичным образом.

При доказательстве деление на целое число можно заменить умножением на обратное заданному, то есть 1 c . Рассмотрим пример свойства на определенных числах.

Пример 4

Разрешено обе части неравенства 4 < 6 умножаем на положительное 0 , 5 , тогда получим неравенство вида − 4 · 0 , 5 < 6 · 0 , 5 , где − 2 < 3 . Когда обе части делим на - 4 , то необходимо изменить знак неравенства на противоположный. отсюда имеем, что неравенство примет вид − 8: (− 4) ≥ 12: (− 4) , где 2 ≥ − 3 .

Теперь сформулируем вытекающие два результата, которые используются при решении неравенств:

• Следствие 1. При смене знаков частей числового неравенства меняется сам знак неравенства на противоположный, как a < b , как − a > − b . Это соответствует правилу умножения обеих частей на - 1 . Оно применимо для перехода. Например, − 6 < − 2 , то 6 > 2 .
• Следствие 2. При замене обратными числами частей числового неравенства на противоположный, меняется и его знак, причем неравенство останется верным. Отсюда имеем, что a и b являются положительными числами, a < b , 1 a > 1 b .

При делении обеих частей неравенства a < b разрешается на число a · b . Данное свойство используется при верном неравенстве 5 > 3 2 имеем, что 1 5 < 2 3 . При отрицательных a и b c условием, что a < b , неравенство 1 a > 1 b может получиться неверным.

Пример 5

Например, − 2 < 3 , однако, - 1 2 > 1 3 являются неверным равенством.

Все пункты объединяет то, что действия над частями неравенства дают верное неравенство на выходе. Рассмотрим свойства, где изначально имеется несколько числовых неравенств, а его результат получим при сложении или умножении его частей.

Определение 9

Когда числа a , b , c , d справедливы для неравенств a < b и c < d , тогда верным считается a + c < b + d . Свойство можно формировать таким образом: почленно складывать числа частей неравенства.

Доказательство 4

Докажем, что (a + c) − (b + d) является отрицательным числом, тогда получим, что a + c < b + d . Из условия имеем, что a < b и c < d . Выше доказанное свойство позволяет прибавлять к обеим частям одинаковое число. Тогда увеличим неравенство a < b на число b , при c < d , получим неравенства вида a + c < b + c и b + c < b + d . Полученное неравенство говорит о том, что ему присуще свойство транзитивности.

Свойство применяется для почленного сложения трех, четырех и более числовых неравенств. Числам a 1 , a 2 , … , a n и b 1 , b 2 , … , b n справедливы неравенства a 1 < b 1 , a 2 < b 2 , … , a n < b n , можно доказать метод математической индукции, получив a 1 + a 2 + … + a n < b 1 + b 2 + … + b n .

Пример 6

Например, при данных трех числовых неравенствах одного знака − 5 < − 2 , − 1 < 12 и 3 < 4 . Свойство позволяет определять то, что − 5 + (− 1) + 3 < − 2 + 12 + 4 является верным.

Определение 10

Почленное умножение обеих частей дает в результате положительное число. При a < b и c < d , где a , b , c и d являются положительными числами, тогда неравенство вида a · c < b · d считается справедливым.

Доказательство 5

Чтобы доказать это, необходимо обе части неравенства a < b умножить на число с, а обе части c < d на b . В итоге получим, что неравенства a · c < b · c и b · c < b · d верные, откуда получим свойство транизитивности a · c < b · d .

Это свойство считается справедливым для количества чисел, на которые необходимо умножить обе части неравенства. Тогда a 1 , a 2 , … , a n и b 1 , b 2 , … , b n являются положительные числами, где a 1 < b 1 , a 2 < b 2 , … , a n < b n , то a 1 · a 2 · … · a n < b 1 · b 2 · … · b n .

Заметим, что при записи неравенств имеются неположительные числа, тогда их почленное умножение приводит к неверным неравенствам.

Пример 7

К примеру, неравенство 1 < 3 и − 5 < − 4 являются верными, а почленное их умножение даст результат в виде 1 · (− 5) < 3 · (− 4) , считается, что − 5 < − 12 это является неверным неравенством.

Следствие: Почленное умножение неравенств a < b с положительными с a и b , причем получается a n < b n .

Свойства числовых неравенств

Рассмотрим ниже приведенную свойства числовых неравенств.

1. a < a , a > a - неверные неравенства,
   a ≤ a , a ≥ a - верные неравенства.
2. Если a < b , то b > a - антисимметричность.
3. Если a < b и b < c то a < c - транзитивность.
4. Если a < b и c - любоое число, то a + b < b + c .
5. Если a < b и c - положительное число, то a · c < b · c ,
   Если a < b и c - отрицательное число, то a · c > b · c .

Следствие 1: если a < b , то - a > - b .

Следствие 2: если a и b - положительные числа и a < b , то 1 a > 1 b .

1. Если a 1 < b 1 , a 2 < b 2 , . . . , a n < b n , то a 1 + a 2 + . . . + a n < b 1 + b 2 + . . . + b n .
2. Если a 1 , a 2 , . . . , a n , b 1 , b 2 , . . . , b n - положительные числа и a 1 < b 1 , a 2 < b 2 , . . . , a n < b n , то a 1 · a 2 · . . . · a n < b 1 · b 2 · . . . b n .

Cледствие 1: если a < b , a и b - положительные числа, то a n < b n .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Например, неравенством является выражение \(x>5\).

Виды неравенств:

Если \(a\) и \(b\) – это числа или , то неравенство называется числовым . Фактически это просто сравнение двух чисел. Такие неравенства подразделяются на верные и неверные .

Например:
\(-5<2\) - верное числовое неравенство, ведь \(-5\) действительно меньше \(2\);

\(17+3\geq 115\) - неверное числовое неравенство, так как \(17+3=20\), а \(20\) меньше \(115\) (а не больше или равно).

Если же \(a\) и \(b\) – это выражения, содержащие переменную, то у нас неравенство с переменной . Такие неравенства разделяют по типам в зависимости от содержимого:

\(2x+1\geq4(5-x)\)				Переменная только в первой степени
\(3x^2-x+5>0\)				Есть переменная во второй степени (квадрате), но нет старших степеней (третьей, четвертой и т.д.)
\(\log_{4}{(x+1)}<3\)
\(2^{x}\leq8^{5x-2}\)

... и так далее.

Что такое решение неравенства?

Если в неравенство вместо переменной подставить какое-нибудь число, то оно превратится в числовое.

Если данное значение для икса превращает исходное неравенство верное числовое, то оно называется решением неравенства . Если же нет - то данное значение решением не является. И чтобы решить неравенство – нужно найти все его решения (или показать, что их нет).

Например, если мы в линейное неравенство \(x+6>10\), подставим вместо икса число \(7\) –получим верное числовое неравенство: \(13>10\). А если подставим \(2\), будет неверное числовое неравенство \(8>10\). То есть \(7\) – это решение исходного неравенства, а \(2\) – нет.

Однако, неравенство \(x+6>10\) имеет и другие решения. Действительно, мы получим верные числовые неравенства при подстановке и \(5\), и \(12\), и \(138\)... И как же нам найти все возможные решения? Для этого используют Для нашего случая имеем:

\(x+6>10\) \(|-6\)
\(x>4\)

То есть нам подойдет любое число больше четырех. Теперь нужно записать ответ. Решения неравенств, как правило, записывают числовыми , дополнительно отмечая их на числовой оси штриховкой. Для нашего случая имеем:

Ответ: \(x\in(4;+\infty)\)

Когда в неравенстве меняется знак?

В неравенствах есть одна большая ловушка, в которую очень «любят» попадаться ученики:

При умножении (или делении) неравенства на отрицательное число, меняется на противоположный («больше» на «меньше», «больше или равно» на «меньше или равно» и так далее)

Почему так происходит? Чтобы это понять, давайте посмотрим преобразования числового неравенства \(3>1\). Оно верное, тройка действительно больше единицы. Сначала попробуем умножить его на любое положительное число, например, двойку:

\(3>1\) \(|\cdot2\)
\(6>2\)

Как видим, после умножения неравенство осталось верным. И на какое бы положительное число мы не умножали – всегда будем получать верное неравенство. А теперь попробуем умножить на отрицательное число, например, минус тройку:

\(3>1\) \(|\cdot(-3)\)
\(-9>-3\)

Получилось неверное неравенство, ведь минус девять меньше, чем минус три! То есть, для того, чтобы неравенство стало верным (а значит, преобразование умножения на отрицательное было «законным»), нужно перевернуть знак сравнения, вот так: \(−9<− 3\).
С делением получится аналогично, можете проверить сами.

Записанное выше правило распространяется на все виды неравенств, а не только на числовые.

Пример: Решить неравенство \(2(x+1)-1<7+8x\)
Решение:

\(2x+2-1<7+8x\)	Перенесем \(8x\) влево, а \(2\) и \(-1\) вправо, не забывая при этом менять знаки
\(2x-8x<7-2+1\)
\(-6x<6\) \(|:(-6)\)	Поделим обе части неравенства на \(-6\), не забыв поменять с «меньше» на «больше»
	Отметим на оси числовой промежуток. Неравенство , поэтому само значение \(-1\) «выкалываем» и в ответ не берем
	Запишем ответ в виде интервала

Ответ: \(x\in(-1;\infty)\)

Неравенства и ОДЗ

Неравенства, также как и уравнения могут иметь ограничения на , то есть на значения икса. Соответственно, из промежутка решений должны быть исключены те значения, которые недопустимы по ОДЗ.

Пример: Решить неравенство \(\sqrt{x+1}<3\)

Решение: Понятно, что для того чтоб левая часть была меньше \(3\), подкоренное выражение должно быть меньше \(9\) (ведь из \(9\) как раз \(3\)). Получаем:

\(x+1<9\) \(|-1\)
\(x<8\)

Все? Нам подойдет любое значение икса меньшее \(8\)? Нет! Потому что если мы возьмем, например, вроде бы подходящее под требование значение \(-5\) – оно решением исходного неравенства не будет, так как приведет нас к вычислению корня из отрицательного числа.

\(\sqrt{-5+1}<3\)
\(\sqrt{-4}<3\)

Поэтому мы должны еще учесть ограничения на значения икса – он не может быть таким, чтоб под корнем было отрицательное число. Таким образом, имеем второе требование на икс:

\(x+1\geq0\)
\(x\geq-1\)

И чтобы икс был окончательным решением, он должен удовлетворять сразу обоим требованиям: он должен быть меньше \(8\) (чтобы быть решением) и больше \(-1\) (чтобы быть допустимым в принципе). Нанося на числовую ось, имеем окончательный ответ:

Ответ: \(\left[-1;8\right)\)