Вот так я вижу выражение главного принципа, всегда обеспечивавшего человечеству громадную скорость, на которой оно безмятежно и вольготно несётся в сторону знака "Стоп! ". Этот принцип можно выразить, конечно, и по-другому: "примем объект "А" за точку " или "тридцатью процентами голосов за другие идеи можно пренебречь ". Можно пренебречь чем угодно , если только это что-то мешает однозначно ответить на интересующие нас вопросы. А таких вопросов много, которые уже много-много лет нас интересуют, и если мы не способны получить на них однозначный ответ, то просто подтасовываем данные так, чтобы однозначный ответ всё-таки получился. Подтасовывание данных чаще всего происходит с помощью упрощения системы; мы пренебрегаем некоторыми данными и получаем определённый результат. Поэтому рождается следующий вопрос. А почему и исходя из каких соображений мы пренебрегли именно этими данными? Может мы просто пытаемся подогнать условия задачи под заранее ожидаемый результат? Почему мы притворяемся, что данных, которыми мы пренебрегаем, не существует в природе и они ни на что не влияют?

"Конечно же влияют , - скажет вам любой математик или физик,- но их влияние абсолютно незначительно. И даже это незначительное влияние мы учитываем, если нам вообще вдруг захочется его учесть, с помощью такого понятия как погрешность ".(очень интересное слово кстати). Но ведь даже из математики известно, что погрешность растёт с ростом количества произведённых действий, подразумевавших пренебрежение какими-то данными. (Если, например, перемножить два числа, которые были округлены с точностью до семи верных знаков после запятой, то получим число, которое уже не будет содержать семи верных знаков после запятой. Т.е. погрешность растёт. ) Тут неучтённый, малю-ю-сенький такой фактор, тут тоже пренебрежём, и так много-много раз. И в итоге мы получаем не просто не точный результат; в нём уже будет заложена недопустимая неточность с точки зрения использования этого результата для решения многих других задач. Но такие результаты зачастую повсеместно принимаются на вооружение и редко кто замечает, что неточность недопустима велика. Ему сразу же приводят пример, для которого использование неточного результата не создаёт никаких проблем. По-крайней мере так кажется на первый взгляд. Когда ошибка вылезет, а случится это может после решения пары-тройки вытекающих из предыдущей логики уравнений, или же это может произойти через несколько сотен лет - придётся возвращаться назад по расчётам и парадигмам вниз, пока мы на каком-то из этапов не увидим недопустимое упрощение.

Поэтому не зря говорят "дьявол в мелочах " и, вполне возможно, что не зря слово "погрешность " имеет в себе явное указание на нечто неблагодарное. Что-то нехорошее мы делаем, получается?

А теперь посмотрите на объём текста, который всего-то навсего описывает искусные выверты и фокусы, которые использует человечество в попытке ответить на интересующие его вопросы. Ведь была возможность поступить по-другому и не пытаться искажать окружающую действительность, подтасовывая данные, и не пытаться искать ответы на все вопросы. Можно было просто понять и смириться с тем, что на некоторые вопросы нам не дано знать ответ хотя бы потому, что человек ещё даже не научился правильно их формулировать. Можно было уже наконец смириться и с тем, что мир намного сложнее, чем наши схематичные представления о нём. Можно уже было смириться и с тем, что техногенный мир, созданный нами, основан на упрощениях, и потому он заведомо проще устроен, и потому не идеален, и ему это можно простить. И нам это тоже можно простить. Можно было уже наконец смириться и с тем, что меньшее не способно познать большее, что менее сложно устроенная система не способна познать более сложно устроенную. И можно было просто жить, любя этот мир таким какой он есть. И любить себя в этом мире и вообще всё, что есть в этом мире. И такие люди есть, уж поверьте=). Но есть и такие, которые не хотят любить - они хотят исследовать, а предмет исследования, тем временем, совсем не торопится покидать категорию "недоисследован " и "к бабке не ходи " ещё на очень и очень долгое время останется для людей непознанным. Разные в общем есть люди.

Что это значит и как это повлияет на решение задачи.

Во первых, разберемся, что такое сопротивление воздуха и почему оно возникает. Как вы знаете (должны знать, вы же ходите в школу), все вещества состоят из молекул или атомов. Атомы это мельчайшие частицы (представим, что это маленькие-маленькие шарики), а молекулы – это тоже маленькие, но уже состоящие из нескольких атомов штуки.

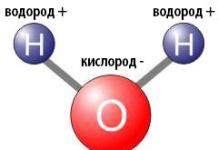
Например молекула воды Н 2 О состоит из двух атомов водорода Н и одного атома кислорода О (то есть три шарика слиплись в одну штуку).

Раз мы до этого сказали, что “все вещества” состоят из них, то и воздух состоит тоже из атомов и молекул (мы дышим кислородом, значит 100% он есть в воздухе). Когда мы бросаем мячик или какой-то предмет вниз, то он начинает сталкиваться с мельчайшими шариками (атомами и молекулами) воздуха. Как раз эти столкновения и называют сопротивлением воздуха.

Теперь попробуем пренебречь этим сопротивлением. Для этого просто-напросто уберем все эти мельчайшие шарики (атомы и молекулы) из воздуха. Согласитесь напоминает вакуум (или безвоздушное пространство)? То есть тела при падении не будут ни с кем сталкиваться, а просто будут лететь вниз.

Теперь разберемся, как это повлияет на решение задачи?

Представим, что мы бросаем с одинаковой высоты мячик и перышко. Что упадет быстрее? Мячик? Нет . Перышко? Нет . Одинаково упадут? Нет . Почему нет? Да потому, что мы не знаем в воздухе это происходит (где есть сопротивление) или в вакууме (нет сопротивления). В воздухе быстрее упадет мячик, так как он тяжелее, и ему проще сбивать со своего пути атомы/молекулы воздуха. А перышко легче, оно будет немного тормозиться при этих столкновениях. Если же мы бросаем их в вакууме, то они упадут одинаково, так как им не придется ни с кем сталкиваться.

Не верите? Смотрите видео (слушать не обязательно, оно на английском).

Вот еще видео на эту же тему

Задача 10016

На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m 1 = 60 кг, масса доски m 2 = 20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) v = 1 м/с? Массой колес и трением пренебречь.

Задача 13147

Тело массой m 1 = 0,25 кг, соединенное невесомой нитью посредством блока (в виде полого тонкостенного цилиндра) с телом массой m 2 = 0,2 кг, скользит по поверхности горизонтального стола. Масса блока m = 0,15 кг Коэффициент трения f тела о поверхность равен 0,2. Пренебрегая трением в подшипниках, определите: 1) ускорение а, с которым будут двигаться эти тела; 2) силы натяжения T 1 и Т 2 нити по обе стороны блока.

Задача 40128

Найти удлинение буксирного троса, жесткость которого равна 100 кН/м, при буксировке автомобиля массой 2 т с ускорением 0,5 м/с 2 . Трением пренебречь.

Задача 25920

На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце стоит человек массой m 1 = 80 кг. С какой скоростью v 2 относительно пола поедет тележка, если человек пойдет по доске со скоростью v 1 = 1 м/с относительно доски? Масса m 2 тележки равна 40 кг. Трением пренебречь.

Задача 11043

Два бруска массами m 1 = 1 кг и m 2 = 4 кг, соединенные шнуром, лежат на столе. С каким ускорением а будут двигаться бруски, если к одному из них приложить силу F = 10 H, направленную горизонтально? Какова будет сила натяжения Т шнура, соединяющего бруски, если силу F = 10 Н приложить к первому бруску? ко второму бруску? Трением пренебречь.

Задача 11108

Камешек скользит с наивысшей точки купола, имеющего форму полусферы. Какую дугу α опишет камешек, прежде чем оторвется от поверхности купола? Трением пренебречь.

Задача 23936

Две одинаковые железнодорожные цистерны сцеплены вместе. Одна из них пустая, а другая с керосином. Масса каждой цистерны с платформой равна 10 т, длина платформы 16 м, масса керосина 60 т. Цистерны соединены шлангом, и керосин по закону сообщающихся сосудов распределился в обеих цистернах поровну. На сколько сместятся цистерны, если они не заторможены? Трением пренебречь.

Задача 16538

С горки высотой h скатывается без проскальзывания шар. Трение пренебрежимо мало. Скорость шара у основания горки вычислили по формуле . Определить погрешность результата. Результат: 1) завышен; 2) занижен; 3) верный.

Задача 19273

На столе лежит гибкая веревка, одна пятая длины которой свободно свисает. Какую работу нужно выполнить, чтобы вытащить эту часть веревки на стол? Длина веревки l = 1 м, а ее масса m = 1 кг. Трением пренебречь.

Энергия, работа, мощность. Законы сохранения в механике.

Поле тяготения. Движение в поле центральных сил.

Элементы специальной теории относительности.

2.1. Примеры решения задач

1. Санки, движущиеся по горизонтальному льду со скоростьюv=2 м/с, въезжают на асфальт (рис. 2.1). Считая, что длина полозьев санок равна ℓ=0,8 м, а коэффициент трения их об асфальт равен μ=0,2, определить путь S, пройденный санками по асфальту, если известно, что S>ℓ. Массу санок считать равномерно распределенной по длине полозьев. Трением санок о лед пренебречь.

Решение . Когда санки въезжают на асфальт, происходит постепенное увеличение силы давления N полозьев на асфальт от нуля до максимального значения, равного силе тяжести mg санок. В связи с этим возрастает и сила трения
, действующая на санки со стороны асфальта.

Поскольку санки движутся под действием переменной силы, воспользуемся для решения задачи понятиями работы и энергии. Работа силы трения, действующей на санки, определяется изменением их кинетической энергии от
доW 2 =0. Тогда на основании соотношения

можно записать

. (1)

С другой стороны, работу А тр можно вычислить по формуле

,

где F тр – сила трения;

α – угол между направлением движения и направлением, действующей силы. В рассматриваемом случае α=180 0 .

Для этого разобьем весь путь S, пройденный санками, на два участка S=ℓ+S " . На пути ℓ на санки действует переменная сила трения
. Найдем совершенную ею работу А 1 . Пусть санки уже прошли по асфальту путь x (рис. 2.1), тогда сила давления полозьев на асфальт равна

,

сила трения

,

а работа этой силы на пути ℓ

. (2)

Интеграл взят со знаком «минус » потому, что величина F тр и dx имеют противоположные знаки. На пути S " сила трения постоянна и равна μmg, и поэтому совершаемая ею работа

.

Полная работа силы трения

. (3)

Приравнивая правые части равенств (1) и (3) и сокращая на массу, найдем

.

Таким образом, весь путь, пройденный санями:

. (4)

м.

Ответ: S =1,42 м.

2. Гиря, положенная на верхний конец спиральной пружины, сжимает ее на x 0 =1,0 мм. На сколько сожмет пружину эта же гиря, брошенная вертикально вниз с высоты h=0,20 м со скоростью v=1,0 м/с?

Решение. Искомая величина x деформации пружины определяется из формулы потенциальной энергии сжатой пружины:

.

Поэтому можно воспользоваться законом сохранения энергии. Так как на гирю действует сила тяжести, рассмотрим систему Земля-гиря-пружина. Поскольку при движении гири и сжатии пружины трения практически не возникает, полная механическая энергия этой изолированной системы будет сохраняться.

Подсчитаем энергию системы в ее начальном (I) и конечном (II) состояниях (рис. 2.2). Выберем за нулевой уровень отсчета высоты самое нижнее положение гири, соответствующее сжатой пружине. В начальном состоянии энергия системы W 1 складывается из потенциальной и кинетической энергии гири:

. (1)

В конечном состоянии у гири не будет кинетической энергии, зато сжатая пружина будет обладать энергией упругой деформации. Таким образом, полная энергия системы W 2 будет равна:

, (2)

Где коэффициент упругой деформации k, согласно его определению, равен

. (3)

Приравнивая по закону сохранения энергии правые части выражений (1) и (2) с учетом соотношения (3), получим после простых преобразований квадратное уравнение относительно x:

Решив уравнение, найдем

.

Отрицательный корень не удовлетворяет условию задачи, так как x<0 означает растяжение пружины, тогда как на самом деле она сжимается.

м.

Ответ: x =8  10 -2 м.

3. Небольшое тело соскальзывает вниз с высоты h=1,0 м по наклонному желобу, переходящему в «мертвую петлю» радиуса R=0,80 м (рис. 2.3). На какой высоте h " выпадает тело из петли? Трением пренебречь.

Решение. Сначала выясним, почему, двигаясь вдоль петли, тело может оторваться от нее. На тело в произвольный момент времени его движения вверх по петле действуют две силы: сила тяжести mg и сила давления N петли, направленная по радиусу к центру окружности. По второму закону Ньютона,

. (1)

Направим оси проекций x и y по векторам нормального и тангенциального ускорений a n a τ , т.е. по радиусу и касательной к окружности. Учитывая, что

и
,

запишем вместо (1) два скалярных уравнений для осей x и y соответственно:

, (2)

. (3)

Так как при движении вверх по петле величина
возрастает, аубывает, то величина
в уравнении (2) должна и подавно убывать. При обращенииN в нуль тело оторвется от петли.

Приняв N=0, перепишем, сокращая величину m, уравнения (2) и (3) для момента отрыва тела от петли:

, (2 ")

. (3 ")

В систему (2 ") и (3 ") явно не вошла искомая величина h " , однако она весьма просто связана с углом α. Как видно из рис. 2.3,

. (4)

Поэтому было бы достаточно найти величину α. Однако найти ее из системы (2 "), (3 ") невозможно, так как эта система содержит более двух неизвестных.

Так как трение отсутствует и, следовательно, на тело действуют только потенциальные силы, то полная механическая энергия тела (точнее: замкнутой системы тело-желоб-Земля) во время его движения будет сохраняться.

В начальный момент времени тело обладает только потенциальной энергией

В момент отрыва движущегося со скоростью v тела его полная энергия

W 2 =
.

Приравняв по закону сохранения энергии величины W 1 и W 2 , получим

. (5)

Теперь из (2 "), (4) и (5), будем иметь

.

Выразив величины, входящие в формулу, в единицах СИ и подставив их числовые значения, получим:

м.

Ответ:
м.

Замечание. Необходимо отметить, что тело выпадает из петли не при любых значениях h. Действительно, так как h " не может быть больше 2R и меньше R (при h "

,
.

Следовательно, при
,
тело из петли не выпадает.

4. На железнодорожной платформе, движущейся по инерции со скоростьюv=10 м/с, укреплено орудие, ствол которого направлен в сторону движения платформы и приподнят над горизонтом на угол α=30 0 (рис. 2.4). Орудие произвело выстрел, в результате чего скорость платформы с орудием уменьшилась в 3 раза. Найти скорость v " снаряда (относительно орудия) при вылете из ствола. Масса снаряда m=10 кг, масса платформы с орудием M=1000 кг.

Решение. На систему платформа с орудием–снаряд извне действуют две силы: сила тяжести системы
и сила нормального давленияN рельсов. До выстрела эти силы уравновешивались, так как система двигалась равномерно. Во время выстрела сила взаимодействия между платформой и рельсами возрастает вследствие явления отдачи, поэтому равновесие сил, приложенных к системе, нарушается:

.

Следовательно, во время выстрела система не является замкнутой, ее импульс изменяется. Однако обе рассматриваемые силы действуют по вертикали, в то время как в горизонтальном направлении никакие силы на систему не действуют (трением платформы о рельсы пренебрегаем). Поэтому проекция импульса системы на горизонтальное направление (на ось x) есть величина постоянная:

. (1)

Пусть состояниям системы до и после выстрела соответствуют значения величины , равныеи
. Рассматривая все движения относительно Земли, получим:

, (2)

, (3)

где
– проекция на осьx скорости v с снаряда относительно Земли.

Чтобы связать величину v с с искомой скоростью v " , будем рассматривать движение снаряда относительно Земли как сложное, состоящее из двух: со скоростью v " относительно орудия и со скоростью v /3 вместе с орудием относительно Земли.

Тогда в соответствии с законом сложения скоростей будем иметь:

. (4)

Спроектируем векторы, входящие в (4), на ось x:

. (5)

Заменив в (3) величину
ее значением по (5) и приравняв согласно (1) правые части формул (2) и (3), найдем

.

Выразив величины, входящие в формулу, в единицах СИ и подставив их числовые значения, получим:

м/с.

Ответ: v " =774 м/с.

5. На корме лодки длиной ℓ=200 см и массой M=120 кг сидит человек массой m=80 кг. В результате кратковременного толчка лодка с человеком приобретает скорость v 0 =2 м/с и начинает двигаться от одного берега канала шириной d=10 м к другому берегу (рис. 2.5), при этом человек переходит с кормы на нос лодки. Пренебрегая сопротивлением воды, найти время движения лодки.

Решение. Рассматривая систему лодка–человек как замкнутую и применяя закон сохранения импульса
, приходим к выводу, что, поскольку закон движения человека относительно лодки нам неизвестен, движение лодки относительно воды (или Земли) нельзя считать равномерным. Однако на основании соотношения
можно утверждать, что скорость центра масс системы относительно воды есть величина постоянная:
. Отсюда следует, что искомое время

, (1)

где С 1 и С 2 – начальное и конечное положения центра инерции системы;

v 0 –скорость центра инерции.

Из формулы (1) следует, что ответ не зависит от характера движения человека. Предположим, что оно было равномерным в течение всего промежутка времени. Тогда будет равномерным и движение лодки. Пусть p 0 и p – импульсы системы соответственно в начальный и некоторый промежуточный моменты времени. Тогда, по закону сохранения импульса,
, т.е.

, (2)

где –скорость лодки;

–скорость человека (все скорости даны в системе отсчета, связанной с Землей).

Решив уравнение (2) относительно t, получим

.

Выразив величины, входящие в формулу, в единицах СИ и подставив их числовые значения, получим:

с.

Ответ: t =4,4 с.

6. На спокойной воде пруда стоит лодка, длиной L и массой M, перпендикулярно берегу, обращенная к нему носом. На корме стоит человек массой m. На какое расстояние S удалится лодка от берега, если человек перейдет с кормы на нос лодки? Трением о воду и о воздух пренебречь.

Решение . Для простоты решения будем считать, что человек идет по лодке с постоянной скоростью. Лодка в этом случае также будет двигаться равномерно. Поэтому путь s, пройденный лодкой относительно берега, определим по формуле:

,

где v – скорость лодки относительно берега;

t – время движения лодки.

Скорость v лодки найдем, пользуясь законом сохранения импульса (количества движения). Так как по условию задачи система человек-лодка изолированная и в начальный момент относительно берега была в покое, то по закону сохранения импульса, опустив знак минус, получим:

,

где u – скорость человека относительно берега.

.

Время t движения лодки равно времени перемещения человека по лодке, т.е.

,

где S – путь, пройденный человеком относительно берега.

Подставив полученные выражения v и t, найдем

.

.

Ответ:
.

7. При выстреле из пружинного пистолета вертикально вверх пуля массой 20г поднялась на высоту 5 м. Определить жесткость k пружины пистолета, если она была сжата на 10 см. Массой пружины пренебречь.

Решение. Для решения задачи воспользуемся законом сохранения энергии в механике. Но прежде проследим за энергетическими превращениями, с которыми связан выстрел.

При зарядке пистолета сжимается пружина. При этом совершается работа A 1 , в результате чего пружина приобретает потенциальную энергию W p1 . При выстреле потенциальная энергия пружины переходит в кинетическую энергию W  2 пули, затем при подъеме ее на высоту h превращается в потенциальную энергию W p 2 пули.

Если пренебречь потерями энергии в этой цепочке энергетических превращений, то на основании закона сохранения энергии можно записать

Выразим работу А 1 . Сила F 1 , сжимающая пружину, является переменной. В каждый данный момент времени она по направлению противоположна силе упругости F и численно равна ей. Сила упругости, возникающая в пружине при ее деформации, определяется по закону Гука:

где x – абсолютная деформация пружины.

Работу переменной силы вычислим как сумму элементарных работ. Элементарная работа при сжатии пружины на dx выразится формулой

dA 1 =F 1 dx,

Интегрируя в пределах от 0 до s, получим

.

Потенциальная энергия пули на высоте h определяется по формуле

где g – ускорение свободного падения.

Таким образом, имеем

.

.

Теперь можем подставить числовые значения и произвести вычисления

Н/м=0,2 кН/м.

Ответ: k=0,2 кН/м.

8. Шар массой m 1 , движущийся горизонтально с некоторой скоростью v 1 , столкнулся с неподвижным шаром массой m 2 . Шары абсолютно упругие, удар прямой, центральный (рис. 2.6). Какую долю своей кинетической энергии первый шар передал второму?

Решение . Доля энергии, переданной первым шаром второму, выразится соотношением

,

где W k1 – кинетическая энергия первого шара до удара;

v 1 – скорость первого шара до удара;

W k2 – кинетическая энергия второго шара после удара;

u 2 – скорость второго шара после удара.

Как видно, для определения  надо найти u 2 . При ударе абсолютно упругих тел одновременно выполняются два закона сохранения: закон сохранения импульса и закон сохранения энергии в механике. Пользуясь этими законами, найдем u 2 .

По закону сохранения импульса, учитывая, что второй шар до удара покоился, имеем:

По закону сохранения энергии

.

Решая совместно данные уравнения, найдем

.

Подставив это выражение в формулу для определения доли  энергии, сократив на v 1 и m 1 , получим

.

Как видно из полученного соотношения, доля переданной энергии зависит только от масс сталкивающихся шаров. Доля передаваемой энергии не изменится, если шары поменяются местами.

Ответ:
.

9. Ящик массой m 1 =20 кг соскальзывает по идеально гладкому лотку длиной =2 м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m 2 =80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении (рис. 2.7). Определить скорость u тележки с ящиком, если лоток наклонен под углом =30 o к рельсам.

Решение . Тележку и ящик можно рассматривать как систему двух неупруго взаимодействующих тел. Но эта система не замкнута, так как сумма внешних сил, действующих на систему: двух сил тяжести m 1 g и m 2 g и силы реакции N 2 , не равна нулю. Поэтому применить закон сохранения импульса к системе "ящик – тележка" нельзя.

Но так как проекция суммы указанных сил на направление оси x, совпадающей с направлением рельсов, равна нулю, то составляющую импульса системы в этом направлении можно считать постоянной, т.е.

,

где p 1x и p 2x – проекции импульса ящика и тележки с песком в момент падения ящика на тележку;

p 1x и p 2x  – те же величины после падения ящика.

Выразим в выше записанном равенстве импульсы тел через их массы и скорости, учтя при этом, что p 2x =0 (тележка до взаимодействия с ящиком покосилась), а также что после взаимодействия оба тела системы движутся с одной и той же скоростью u:

где v 1 – скорость ящика перед падением на тележку;

v 1x =v 1 cos – проекция этой скорости на ось x.

Отсюда выразим искомую скорость:

.

Скорость v 1 ящика перед падением определим из закона сохранения энергии

,

где h=sin.

После сокращения на m 1 найдем

.

Подставив найденное выражение для v 1 в формулу для скорости u, получим

.

Предварительно проверив размерность полученного результата, подставим числовые значения и произведем вычисления:

Ответ: u=0,77 м/с.

10. При упругом ударе нейтрона о ядро углерода он движется после удара в направлении, перпендикулярном к начальному. Считая, что масса М ядра углерода в n=12 раз больше массы m нейтрона, определить, во сколько раз уменьшается энергия нейтрона в результате удара.

Решение. Введем обозначения: v –скорость нейтрона до удара, v " –скорость нейтрона после удара, V –скорость ядра углерода после удара (до удара она равна нулю).

В результате упругого удара импульс и энергия, которыми до удара обладал нейтрон, распределяются между двумя частицами. При этом по законам сохранения импульса и энергии соответственно имеем:

, (1)

. (2)

По условию задачи требуется найти отношение

.

Для выполнения расчетов необходимо перейти от векторной формы записи уравнения (1) к скалярной форме. Это можно сделать, применив метод проекций, который неоднократно использовался. Однако в данном случае можно поступить проще. Изобразим на рисунке 2.8 импульсыmv " , MV и их векторную сумму mv , учитывая, что угол между векторами mv и mv " равен π/2. Из треугольника импульсов имеем

Почленно разделив уравнение (2) на m и (3) на m 2 и учитывая условие M/m=n, получим:

, (4)

. (5)

Чтобы исключить из системы величину V, разделим почленно (5) на (4):

,

а числитель и знаменатель полученного соотношения на (v ") 2 , тогда находим

,

.

Ответ: α=1,2.

11. Молот массой 5,00 кг, двигаясь со скоростью v=4,00 м/с, ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе с изделием равна M=95 кг. Считая удар абсолютно неупругим, определить энергию, расходуемую на ковку (деформацию) изделия. Чему равен КПД процесса ковки при данных условиях?

Решение. Строго говоря, система молот–изделие–наковальня не является замкнутой. На нее действуют извне сила тяжести (M+m)g и сила давления N опоры, на которой стоит наковальня. Во время удара молота вторая сила в той или иной степени, определяемой упругими свойствами опоры, будет превышать первую силу и к рассматриваемой системе будет приложена извне равнодействующая

Однако силы ударного взаимодействия тел весьма велики. Очевидно, условие задачи предполагает, что по сравнению с этими силами величиной R можно пренебречь, и, таким образом, считать систему замкнутой.

На основании закона сохранения энергии можно утверждать, что энергия, затраченная на деформацию изделия, равна разности значений механической энергии до и после удара. Так как во время удара изменяется только кинетическая энергия тел (незначительным перемещением тел по вертикали за время удара мы пренебрегаем), то для энергии деформации получаем

, (1)

где v " –общая скорость всех тел системы после неупругого удара, которую можно определить на основании закона сохранения импульса:

. (2)

.

Подставив в формулу (1) значение v " , получим:

. (3)

Так как энергия, расходуемая на ковку изделия, является по смыслу задачи полезной, то КПД процесса ковки

. (4)

Подставив числовые значения заданных величин в формулы (3) и (4) и выполнив вычисление, получим:

Дж;

.

Ответ:
Дж;
.

Замечание. Из формулы (4) видно, что КПД процесса ковки тем больше, чем больше масса наковальни по сравнению с массой молота. При (m / M )  0 η  1.

12. Маховик, выполненный в виде диска радиусом 0,4 м и имеющий массу 1 кг, раскручен до скорости вращения 480 об/мин и предоставлен самому себе. Под действием трения вала о подшипники он до полной остановки сделал 240 оборотов. Определить момент сил трения вала о подшипники.

Решение . Так как в условии задачи дано число оборотов, сделанных маховиком до полной остановки, то воспользуемся уравнением, выражающим связь между работой и изменением кинетической энергии, для вращательного движения:

где А=М – работа сил трения;

–изменение кинетической энергии;

 – угол поворота;

–момент инерции маховика относительно данной оси вращения;

 1 и  2 – начальная и конечная угловые скорости маховика, при этом  2 =0.

.

Размерность полученного результата очевидна. Подставим в полученное для M 2 выражение числовые значения входящих величин и произведем вычисления:

Нм.

Знак «минус » означает, что на маховик действительно действуют силы трения.

Ответ: М 2 =-6,7 Нм.

13. Платформа в виде сплошного диска радиусом R=1,5 м и массой m 1 =180 кг вращается по инерции около вертикальной оси с частотой n=10 мин -1 (рис. 2.9). В центре платформы стоит человек массой m 2 =60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?

Решение . Платформа вращается по инерции. Следовательно, момент внешних сил относительно оси вращения z, совпадающей с гео- метрической осью платформы, равен нулю. При этом условии момент импульса L z системы "платформа-человек" остается постоянным:

L z =I z =const,

где I z – момент инерции платформы с человеком относительно оси z;

 – угловая скорость платформы.

Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому

где I 1 –момент инерции платформы;

I 2 –момент инерции человека.

С учетом этого имеем

(I 1 +I 2)=const

(I 1 +I 2)=(I 1 +I 2 ),

где нештрихованные значения величин относятся к начальному состоянию системы, штрихованные – к конечному состоянию.

Момент инерции платформы (сплошного диска) относительно оси z при переходе человека не изменятся:

.

Момент инерции человека будет изменяться. Если человека рассматривать как материальную точку, то его момент инерции I z в начальном положении (в центре платформы) можно считать равным нулю. В конечном положении (на краю платформы) момент инерции человека

.

Подставим в формулу закона сохранения найденные выражения моментов инерции, начальную угловую скорость вращения платформы с человеком, выраженную через частоту вращения n (=2n) и конечную угловую скорость, выраженную через линейную скорость v человека относительно пола (=v/R), получим:

.

После простых преобразований находим интересующую нас скорость:

.

Проверив размерность полученного результата, подставим числовые значения физических величин в системе СИ, произведем вычисления:

Ответ: v=0,96 м/с.

14. Круглая платформа радиуса R=1,00 м, момент инерции которой I=130 кгм 2 , вращается по инерции вокруг вертикальной оси, делая n 1 =1,00 об/с. На краю платформы стоит человек, масса которого m=70 кг (рис. 2.10). Сколько оборотов в секунду n 2 будет совершать платформа, если человек перейдет в ее центр? Момент инерции человека рассчитывать как для материальной точки.

Решение. Перемещаясь по платформе, человек взаимодействует с ней. О характере этого взаимодействия нам ничего не известно, поэтому основное уравнение динамики вращательного движения к платформе применить невозможно. В этой задаче нет оснований и для применения закона сохранения энергии, поскольку не исключено, что, перемещаясь по вращающейся платформе, человек будет совершать работу, изменяя механическую энергию вращающейся системы платформа–человек .

Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы платформа–человек выполняется закон сохранения момента импульса, который запишем так:

. (1)

Начальный момент импульса системы L 1 (человек стоит на краю платформы) и конечный момент импульса L 2 (человек стоит в центре платформы) соответственно равны:

где
– момент инерции человека;

–начальный момент инерции системы;

I – момент инерции платформы;

ω 1 – начальная угловая скорость системы;

n 1 – начальное число оборотов системы;

I 2 =I – конечный момент инерции системы;

ω 2 – конечная угловая скорость системы;

n 2 – конечное число оборотов системы.

Решая систему уравнений (1)–(3), для конечного числа оборотов системы будем иметь:

.

Проверив размерность полученного результата, подставив числовые значения физических величин в системе СИ, произведем вычисления:

об/с.

Ответ: n 2 =1,54 об/с.

15. Маховик, имеющий вид диска радиусаR и массы М, может вращаться вокруг горизонтальной оси. К его цилиндрической поверхности прикреплен шнур, к другому концу которого подвешен груз массы m. Груз был поднят и затем отпущен. Упав свободно с высоты h, груз натянул шнур и благодаря этому привел маховик во вращение (рис. 2.11). Какую угловую скорость ω приобрел при этом маховик?

Решение. Когда падающий груз натягивает шнур, возникает взаимодействие посредством шнура между грузом и маховиком. Характер взаимодействия зависит от упругих свойств тел (в основном шнура). В результате этого взаимодействия увеличивается скорость точек цилиндрической поверхности маховика и уменьшается скорость падения гири. Шнур растягивается до тех пор пока эти скорости не станут одинаковыми. Такое кратковременное взаимодействие груза и маховика можно рассматривать как неупругий удар. При неупругом ударе закон сохранения механической энергии не выполняется. Следовательно, для решения этой задачи данный закон неприменим. Однако к системе груз–маховик можно применить закон сохранения момента импульса.

На рассматриваемую систему действуют три внешних силы: сила тяжести маховика, реакция опоры и сила тяжести груза. Поскольку две первые силы проходят перпендикулярно оси диска, их момент относительно этой оси равен нулю. Действием же момента силы тяжести груза, равного mgR, во время удара можно пренебречь по сравнению с моментом сил взаимодействия груза и маховика при ударе. Таким образом, можно считать, что результирующий момент всех внешних сил относительно оси маховика во время удара равным нулю. Тогда, по закону сохранения момента импульса,

, (1)

где L 1 и L 2 – моменты импульса системы груз – маховик соответственно в начале и в конце удара.

Так как в начале удара диск был еще неподвижен, величина L 1 представляет собой момент импульса падающего груза относительно оси вращения маховика. Принимая груз за материальную точку, можно записать

, (2)

где v 1 – скорость гири, которую можно найти по известной формуле скорости при свободном падении:

. (3)

Величина L 2 равна суммарному моменту импульса гири и вращающегося маховика, когда скорости груза и точек цилиндрической поверхности диска стали одинаковыми:

, (4)

где величины v 2 и ω связаны соотношением

. (5)

Подставив в уравнение (1) значения L 1 и L 2 . Решив его относительно ω с учетом формул (3), (5) и
, получим

.

Ответ:
.

16. Маятник в виде однородного шара, жестко скрепленный с тонким стержнем, длина которого равна радиусу шара, может совершать колебательные движения вокруг горизонтальной оси, проходящей через конец стержня (рис. 2.12). В шар нормально к его поверхности ударилась пуля массыm=10,0 г, летевшая горизонтально со скоростью v=800 м/с, и застряла в шаре. Масса шара М=10,0 кг, его радиус R=15 см. На какой угол α отклонится маятник в результате удара пули? Массой стержня пренебречь.

Решение. Как видно из рисунка, искомый угол α связан с высотой h подъема центра шара:

. (1)

Так как величина h определяет потенциальную энергию, полученную шаром вследствие удара пули. Поскольку в результате удара пули в шар скорости обоих тел будут одинаковыми, то удар следует считать неупругим. Следовательно, механическая энергия в процессе удара не сохраняется (частично переходит во внутреннюю энергию). Однако после удара механическая энергия движущейся системы маятник–пуля будет сохраняться, так как теперь в ней действуют только потенциальные силы. Таким образом, при подъеме шара вместе с пулей кинетическая энергия вращательного движения системы будет превращаться в потенциальную энергию поднятых тел. По закону сохранения энергии,

, (2)

где I – момент инерции маятника вместе с застрявшей в нем пулей;

h " – высота подъема пули.

По условию задачи M>>m, поэтому, пренебрегая массой пули по сравнению с массой шара, величиной
в уравнении (2) можно пренебречь.

Для момента инерции маятника, на основании теоремы Штейнера, будем иметь:

Для определения угловой скорости ω воспользуемся законом сохранения момента импульса. Его применение основано на том, что во время удара на систему маятник–пуля извне действуют силы тяжести и реакции опоры. Вторая сила проходит перпендикулярно оси маятника, поэтому ее момент равен нулю. Учитывая, что за время удара маятник не успевает заметно отклониться от вертикали, и принимая во внимание условие M>>m, можно считать, что и первая сила во время удара тоже проходит перпендикулярно оси вращения. Следовательно, ее момент также равен нулю.

Согласно закону сохранения момента импульса системы во время удара, должно выполняться соотношение:

, (4)

где , и– моменты импульса системы соответственно в начале м в конце процесса удара.

Величина есть момент импульса летящей пули относительно оси вращения маятника (сам маятник пока еще неподвижен). На основании определения имеем

. (5)

Момент импульса маятника с застрявшей в нем пулей, согласно определению, равен

. (6)

Решая систему уравнений (4)–(6), получаем для угловой скорости

. (7)

Исключив из системы (1)–(3), (7) неизвестные I, ω и h, найдем

.

Подставив в эту формулу числовые значения величин, выраженные в единицах СИ, и произведя вычисления, получим:

; α=26 0 .

Ответ: α=26 0 .

17. Через блок, выполненный в виде диска и имеющий массу m=80 г, перекинута тонкая, гибкая нить, к концам которой подвешены грузы с массами m 1 =100 г и m 2 =200 г (рис. 2.13). С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.

Решение . Применим к решению задачи закон сохранения энергии, согласно которому при отсутствии трения полная энергия изолированной системы остается неизменной. Энергия при этом может превращаться только из потенциальной в кинетическую, и наоборот. Напомним, что в механике полной энергией тела называется сумма его потенциальной и кинетической энергий.

Предположим, что в начальный момент движения потенциальная энергия первого груза была равна W p1 , второго – W p2 . Через некоторое время высота первого груза увеличилась на h, второго уменьшилась на h. Потенциальная энергия первого груза стала равна

W 1 =W p1 + m 1 gh,

W 2 =W p2 – m 2 gh.

Кроме того, каждый из грузов, двигаясь с ускорением a , приобрел за это время скорость v и кинетическую энергию, равную соответственно

и
.

Точно так же диск, вращаясь равноускоренно, приобрел угловую скорость и соответствующую ей кинетическую энергию

,

где
– момент инерции диска;

–угловая скорость.

Тогда для кинетической энергии диска, после соответствующих преобразований, будем иметь

.

Закон сохранения импульса целесообразно применять для решения тех задач, в которых требуется определять скорости, а не силы или ускорения. Конечно, решать подобные задачи можно, используя законы Ньютона. Но применение закона сохранения импульса упрощает решение.

Прежде чем решать задачу с помощью закона сохранения импульса, надо выяснить, можно ли его применять в данном случае. Закон можно применять для замкнутой системы или же в случае, когда сумма проекций сил на какое-либо направление равна нулю, а также когда импульсом внешних сил можно пренебречь.

Для решения задачи нужно записать закон в векторной форме (5.3.7).

После этого векторное уравнение записывают в проекциях на оси выбранной системы координат(1).

Выбор направления осей диктуется удобством решения задачи. Если, например, все тела движутся вдоль одной прямой, то координатную ось целесообразно направить вдоль этой прямой.

При решении некоторых задач приходится использовать дополнительно уравнения кинематики.

Некоторые задачи решаются с применением уравнения изменения импульса в форме (5.3.5).

Задача 1

Стальной шарик массой 0,05 кг падает с высоты 5 м на стальную плиту. После столкновения шарик отскакивает от плиты с такой же по модулю скоростью. Найдите силу, действующую на плиту при ударе, считая ее постоянной. Время соударения равно 0,01 с.

Решение. При ударе шар и плита действуют друг на друга с силами, равными по модулю, но противоположными по направлению. Определив силу, действующую на шарик со стороны плиты, мы тем самым найдем силу, с которой шарик действовал на плиту за время Δt, в течение которого длится соударение.

Во время соударения на шарик действуют две силы: сила тяжести m и сила со стороны плиты (рис. 5.13).

Рис. 5.13

Согласно уравнению (5.2.3)

Обозначим через 1 скорость шарика непосредственно до удара о плиту, а через 2 - скорость после удара, тогда изменение импульса шарика Δ = m 2 - m 1 , поэтому

В проекциях на ось У это уравнение запишется так:

Учитывая, что v 2 = v 1 = v, получим

Модуль скорости шарика при падении его с высоты h определяется по формуле v = = 10 м/с. Теперь, используя выражение (5.7.1), найдем модуль силы :

По третьему закону Ньютона

Следовательно, F 1 = 100,5 Н; эта сила приложена к плите и направлена вниз.

Заметим, что чем меньше время взаимодействия Δt, тем большим будет значение величины в формуле (5.7.1) по сравнению с mg. Поэтому при соударении можно не учитывать силу тяжести. Если бы шар был сделан из пластилина, то он бы прилип к плите и модуль изменения его импульса был бы в два раза меньше. Соответственно и сила, действующая на плиту, была бы также в два раза меньше.

Задача 2

Во время маневров на железнодорожной станции две платформы массами m 1 = 2,4 10 4 кг и m 2 = 1,6 10 4 кг двигались навстречу друг другу со скоростями, модули которых равны v 1 = 0,5 м/с и v 2 = 1 м/с. Найдите скорость их совместного движения после того, как сработала автосцепка.

Решение. Изобразим схематично движущиеся платформы до столкновения (рис. 5.14). Внешние силы 1 и m 1 , 2 и m 2 , действующие на тела системы, взаимно уравновешены. На платформы действуют еще силы трения, которые являются внешними для системы.

Рис. 5.14

При качении платформ по рельсам силы трения невелики, поэтому за малый интервал времени столкновения они заметно не изменят импульс системы. Следовательно, можно применить закон сохранения импульса:

где - скорость платформ после сцепки.

В проекциях на ось X имеем:

Так как v 1х = v 1 a v 2x = -v 2 , то

Отрицательный знак проекции скорости показывает, что скорость направлена противоположно оси X (справа налево).

Задача 3

Два пластилиновых шарика, отношение масс которых = 4, после соударения слиплись и стали двигаться по гладкой горизонтальной поверхности со скоростью . (рис. 5.15, вид сверху).

Рис. 5.15

Определите скорость легкого шара до соударения(2), если он двигался втрое быстрее тяжелого (v 1 = Зv 2), а направления движения шаров были взаимно перпендикулярны. Трением пренебречь.

Решение. Так как скорости 1 и 2 шаров взаимно перпендикулярны, то оси прямоугольной системы координат удобно направить параллельно этим скоростям.

Согласно закону сохранения импульса имеем:

Запишем это уравнение в проекциях на оси X и У, проведенные так, как показано на рисунке 5.15:

Так как v 1x = v 1 , v 2x = 0, v 1y = 0 и v 2y = v 2 , то

Модуль скорости равен:

Итак, v 1 = u, следовательно, v 1 = Зu.

Задача 4

Кузнечик сидит на конце соломинки длиной l, которая лежит на гладком полу. Кузнечик прыгает и попадает на другой конец соломинки. С какой минимальной начальной скоростью относительно пола min он должен прыгнуть, если его масса М, а масса соломинки m. Сопротивление воздуха и трение не учитывать.

Решение. Направим ось У вверх, а ось X вдоль соломинки по направлению прыжка кузнечика (рис. 5.16). Проекции скорости v кузнечика на координатные оси соответственно равны:

v x = vcos α и v y = vsin α.

Рис. 5.16

Рассмотрим систему кузнечик - соломинка. На тела системы внешние силы действуют лишь по вертикальному направлению (трение отсутствует).

Так как сумма проекций внешних сил на ось X равна нулю, то сохраняется сумма проекций импульсов кузнечика и соломинки на ось X:

где v 1x - проекция скорости соломинки относительно пола. Отсюда

По горизонтальному направлению кузнечик относительно соломинки пролетит расстояние l.

Следовательно, модуль горизонтальной составляющей его скорости относительно движущейся соломинки равен:

Но с другой стороны,

Таким образом,

Очевидно, что модуль скорости кузнечика минимален тогда, когда максимален знаменатель дроби полученного выражения. Как известно, значение синуса не может быть больше 1. Итак,

Задача 5

В начальный момент времени ракета массой М имела скорость v0. В конце каждой секунды из ракеты выбрасывается порция газа массой m. Скорость порции газа отличается от скорости ракеты до сгорания данной массы газа на постоянное значение, равное u, т. е. скорость истечения газа постоянна. Определите скорость ракеты через n секунд. Действие силы тяжести не учитывать.

Решение. Обозначим через v k скорость ракеты в конце k-й секунды. В конце (k + 1)-й секунды из ракеты выбрасывается газ массой m, который уносит с собой импульс, равный m(-u + v k). Из закона сохранения импульса, записанного для модулей векторов, следует, что

Изменение скорости ракеты за 1 с равно:

Зная изменение скорости за 1 с, можно написать выражение для скорости в конце n-й секунды:

Упражнение 10

1. Свинцовый шар массой 200 г движется перпендикулярно стене со скоростью 10 м/с и сталкивается с ней. Найдите силу, действующую на стену при ударе, считая ее постоянной. Время столкновения равно 0,01 с. Шар не отскакивает от стены.
2. Стальной шар массой 100 г движется по горизонтальной поверхности без трения в направлении, перпендикулярном стене. Скорость шара до удара равна 10 м/с. После соударения шар отскакивает от стены с такой же по модулю скоростью, но в противоположном направлении. Найдите силу, действующую на стену при ударе, считая ее постоянной. Время соударения 0,01 с.
3. По рельсам в горизонтальном направлении катится тележка с песком. Через отверстие в дне песок ссыпается между рельсами. Изменяется ли скорость тележки? Трение не учитывать.
4. На платформу массой 600 кг, движущуюся горизонтально со скоростью 1 м/с, насыпали сверху 200 кг щебня. Чему стала равна скорость платформы?
5. Ракета, масса которой вместе с зарядом равна 250 г, взлетает вертикально вверх и достигает высоты 150 м. Определите скорость истечения газов из ракеты, считая, что сгорание заряда происходит мгновенно. Масса заряда равна 50 г.
6. Призма массой М с углом наклона а находится на гладком льду. На призме у ее основания стоит собака массой m. С какой скоростью будет двигаться призма, если собака побежит вверх по призме со скоростью v относительно нее?
7. Граната, брошенная от поверхности Земли, разрывается на два одинаковых осколка в наивысшей точке траектории на расстоянии а от места бросания, считая по горизонтали. Один из осколков летит в обратном направлении с той же по модулю скоростью, которую имела граната до разрыва. На каком расстоянии l от места бросания упадет второй осколок?
8. Две ракеты массой М каждая летят в одном направлении: одна со скоростью v, а другая со скоростью v 1 = 1.1v. Когда одна ракета догнала другую, на короткое время был включен двигатель первой ракеты. Какую массу отработанного топлива она должна выбросить со скоростью v 2 = Зу относительно ракеты, чтобы скорости ракет для совершения безопасной стыковки стали равными?
9. Две лодки идут параллельными курсами навстречу друг другу с одинаковыми по модулю скоростями. При встрече лодки обмениваются грузами, имеющими одинаковую массу. Обмен может происходить двумя способами: 1) сначала с одной лодки на другую перебрасывают груз, а затем со второй лодки перебрасывают груз обратно на первую; 2) грузы перебрасывают из лодки в лодку одновременно. При каком способе скорость лодок после перебрасывания грузов будет больше?
10. Три лодки с одинаковыми массами М движутся по инерции друг за другом с одинаковыми скоростями v. Из средней лодки в крайние одновременно перебрасывают грузы массой m со скоростью u относительно лодок. Какие скорости будут иметь лодки после перебрасывания грузов? Сопротивление воды и присоединенную массу не учитывать.
11. Снаряд разрывается в верхней точке траектории на две равные части. Одна половина снаряда получает скорость, направленную вертикально вниз, и падает под местом разрыва, а вторая половина снаряда оказывается на расстоянии l по горизонтали от этого места. Определите модуль скорости снаряда перед разрывом и модуль скорости второго осколка, если известно, что взрыв произошел на высоте Н и первый осколок достиг поверхности Земли через промежуток времени, равный t.
12. Человек, находящийся в лодке, переходит с ее носовой части на корму. На какое расстояние относительно воды переместится лодка длиной l, если масса человека m 1 а масса лодки m 2 ? Сопротивление воды и присоединенную массу не учитывать.

(1) Иногда целесообразно решать задачу, используя закон сложения векторов.

(2) Если после соударения тела движутся с одинаковой скоростью, то такой удар называется абсолютно неупругим.